Naravni pojavi in procesi okoli nas so precej zapleteni. Za njihov natančen fizični opis je treba uporabiti okoren matematični aparat in upoštevati veliko število pomembnih dejavnikov. Da bi se izognili tej težavi, se v fiziki uporabljajo nekateri poenostavljeni modeli, ki močno olajšajo matematično analizo procesa, vendar praktično ne vplivajo na natančnost njegovega opisa. Eden od njih je model idealnega plina. Podrobneje razmislimo o tem v članku.
Koncept idealnega plina
Idealni plin je agregacijsko stanje snovi, ki je sestavljeno iz materialnih točk, ki med seboj ne delujejo. Pojasnimo to definicijo podrobneje.
Najprej govorimo o materialnih točkah kot o objektih, ki sestavljajo idealen plin. To pomeni, da njegove molekule in atomi nimajo velikosti, ampak imajo določeno maso. To je krepkolahko naredimo približek ob upoštevanju dejstva, da je pri vseh realnih plinih pri nizkih tlakih in visokih temperaturah razdalja med molekulami veliko večja od njihovih linearnih dimenzij.
Drugič, molekule v idealnem plinu ne bi smele medsebojno delovati. V resnici takšne interakcije vedno obstajajo. Torej, celo atomi žlahtnih plinov doživljajo dipol-dipolno privlačnost. Z drugimi besedami, prisotne so van der Waalsove interakcije. Vendar pa so te interakcije v primerjavi s kinetično energijo vrtenja in translacijskega gibanja molekul tako majhne, da ne vplivajo na lastnosti plinov. Zato jih ni mogoče upoštevati pri reševanju praktičnih problemov.
Pomembno je omeniti, da se vsi plini, v katerih je gostota nizka in visoka temperatura, ne morejo šteti za idealne. Poleg van der Waalsovih interakcij obstajajo tudi druge, močnejše vrste vezi, na primer vodikove vezi med H2O molekulami, ki vodijo do hude kršitve pogojev idealnosti plina. Zaradi tega vodna para ni idealen plin, ampak zrak.
Fizični model idealnega plina
Ta model lahko predstavimo na naslednji način: predpostavimo, da plinski sistem vsebuje N delcev. To so lahko atomi in molekule različnih kemikalij in elementov. Število N delcev je veliko, zato se za njegovo opisovanje običajno uporablja enota "mol" (1 mol ustreza Avogadrovemu številu). Vsi se gibljejo v nekem obsegu V. Gibanje delcevso kaotični in neodvisni drug od drugega. Vsak od njih ima določeno hitrost v in se premika po ravni poti.
Teoretično je verjetnost trka med delci skoraj nič, saj je njihova velikost majhna v primerjavi z razdaljami med delci. Če pa pride do takšnega trka, potem je popolnoma elastičen. V slednjem primeru se skupni zagon delcev in njihova kinetična energija ohranita.
Obravnavani model idealnih plinov je klasičen sistem z velikim številom elementov. Zato sta hitrost in energija delcev v njej podvrženi statistični porazdelitvi Maxwell-Boltzmanna. Nekateri delci imajo nizke hitrosti, drugi pa visoke. V tem primeru obstaja določena ozka omejitev hitrosti, v kateri so najverjetnejše vrednosti te količine. Porazdelitev hitrosti molekul dušika je shematično prikazana spodaj.
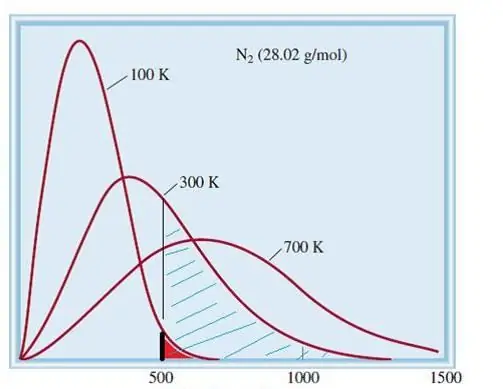
Kinetična teorija plinov
Model idealnih plinov, opisan zgoraj, edinstveno določa lastnosti plinov. Ta model je prvi predlagal Daniel Bernoulli leta 1738.

Pozneje so ga do današnjega stanja razvili August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski in drugi znanstveniki.
Kinetična teorija tekočih snovi, na podlagi katere je zgrajen model idealnega plina, pojasnjuje dve pomembni makroskopski lastnosti sistema na podlagi njegovega mikroskopskega obnašanja:
- Tlak v plinih je posledica trka delcev s stenami posode.
- Temperatura v sistemu je rezultat manifestacije nenehnega gibanja molekul in atomov.
Razširimo oba zaključka kinetične teorije.
tlak plina
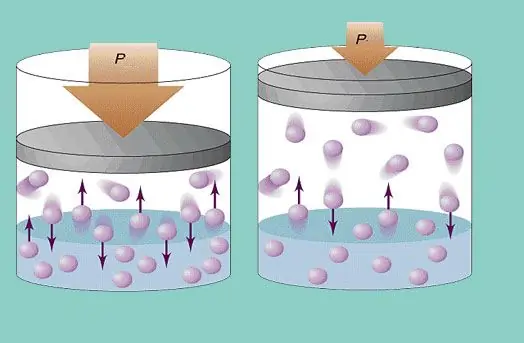
Model idealnega plina predpostavlja stalno kaotično gibanje delcev v sistemu in njihovo nenehno trčenje s stenami posode. Vsak tak trk velja za absolutno elastičnega. Masa delcev je majhna (≈10-27-10-25 kg). Zato pri trčenju ne more ustvariti velikega pritiska. Kljub temu je število delcev in s tem število trkov ogromno (≈1023). Poleg tega je povprečna kvadratna hitrost elementov nekaj sto metrov na sekundo pri sobni temperaturi. Vse to vodi do ustvarjanja znatnega pritiska na stene posode. Lahko se izračuna z naslednjo formulo:
P=Nmvcp2 / (3V), kjer je vcp povprečna kvadratna hitrost, m je masa delcev.
Absolutna temperatura
V skladu z modelom idealnega plina je temperatura edinstveno določena s povprečno kinetično energijo molekule ali atoma v preučevanem sistemu. Napišete lahko naslednji izraz, ki povezuje kinetično energijo in absolutno temperaturo za idealen plin:
mvcp2 / 2=3 / 2kB T.
Tukaj je kB Boltzmannova konstanta. Iz te enakosti dobimo:
T=m vcp2 / (3kB).
Univerzalna enačba stanja
Če združimo zgornje izraze za absolutni tlak P in absolutno temperaturo T, lahko zapišemo naslednjo enakost:
PV=nRT.
Tukaj je n količina snovi v molih, R je plinska konstanta, ki jo je uvedel D. I. Mendelejev. Ta izraz je najpomembnejša enačba v teoriji idealnih plinov, ker združuje tri termodinamične parametre (V, P, T) in ni odvisen od kemijskih lastnosti plinskega sistema.

Univerzalno enačbo je prvi eksperimentalno izpeljal francoski fizik Emile Clapeyron v 19. stoletju, nato pa jo je v sodobno obliko pripeljal ruski kemik Mendeljejev, zato trenutno nosi imena teh znanstvenikov.






