Plini so z vidika termodinamike opisani z nizom makroskopskih značilnosti, med katerimi so glavne temperatura, tlak in prostornina. Stalnost enega od teh parametrov in sprememba drugih dveh kaže, da se v plinu pojavlja en ali drug izoproces. Ta članek bomo posvetili podrobnemu odgovoru na vprašanja, da je to izohoričen proces, kako se razlikuje od izotermnih in izobaričnih sprememb stanj plinskega sistema.
Idealni plin v fiziki

Preden odgovorite na vprašanje, da je to izohoričen proces, bi morali bolje spoznati koncept idealnega plina. V fiziki se razume kot vsak plin, v katerem povprečna kinetična energija njegovih sestavnih delcev daleč presega potencialno energijo njihove interakcije, razdalje med temi delci pa so za nekaj redov velikosti večje od njihovih linearnih dimenzij. Pod navedenimi pogoji je možno pri izvedbiizračuni ne upoštevajo interakcijske energije med delci (enaka je nič), lahko pa tudi domnevamo, da so delci materialne točke z določeno maso m.
Edini proces, ki poteka v idealnem plinu, je trk delcev s stenami posode, ki vsebuje snov. Ti trki se v praksi kažejo kot obstoj določenega tlaka v plinu P.
Praviloma se lahko vsaka plinasta snov, ki je sestavljena iz relativno kemično inertnih molekul in ima nizek tlak in visoke temperature, šteje za idealen plin z zadostno natančnostjo za praktične izračune.
Enčba, ki opisuje idealen plin
Seveda govorimo o univerzalnem zakonu Clapeyron-Mendelejeva, ki ga je treba dobro razumeti, da bi razumeli, da je to izohoričen proces. Torej ima univerzalna enačba stanja naslednjo obliko:
PV=nRT.
To pomeni, da je produkt tlaka P in prostornine plina V enak zmnožku absolutne temperature T in količine snovi v molih n, kjer je R faktor sorazmernosti. Samo enačbo je prvi zapisal Emile Clapeyron leta 1834, v 70. letih 19. stoletja pa je D. Mendelejev vanjo zamenjal niz konstantnih vrednosti ene same univerzalne plinske konstante R (8,314 J/(molK).)).
Skladno z enačbo Clapeyron-Mendelejeva v zaprtem sistemu ostane število plinskih delcev konstantno, zato se lahko spremenijo le trije makroskopski parametri (T, Pin V). Slednje dejstvo je osnova za razumevanje različnih izoprocesov, ki bodo obravnavani v nadaljevanju.
Kaj je izohorični proces?
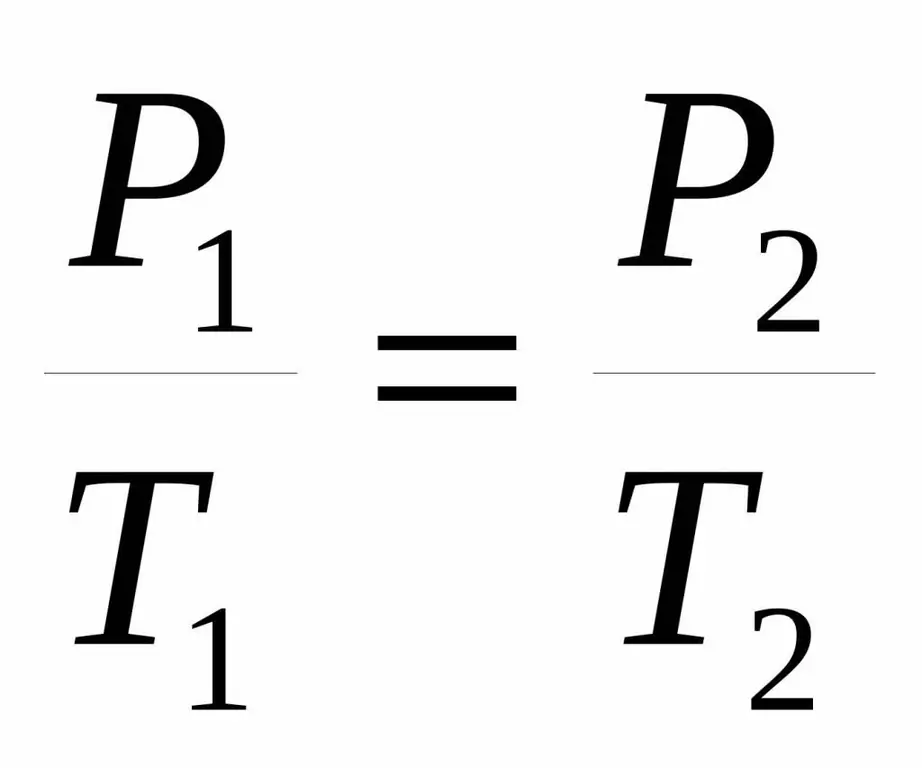
Ta proces se razume kot absolutno kakršna koli sprememba stanja sistema, v katerem je ohranjena njegova prostornina.
Če se obrnemo na univerzalno enačbo stanja, lahko rečemo, da se v izohoričnem procesu v plinu spreminjata le tlak in absolutna temperatura. Da bi natančno razumeli, kako se termodinamični parametri spreminjajo, zapišemo ustrezen matematični izraz:
P / T=konst.
Včasih je ta enakost podana v nekoliko drugačni obliki:
P1 / T1=P2 / T 2.
Obe enakosti se imenujeta Charlesov zakon po imenu francoskega znanstvenika, ki je konec 18. stoletja eksperimentalno pridobil omenjeno odvisnost.

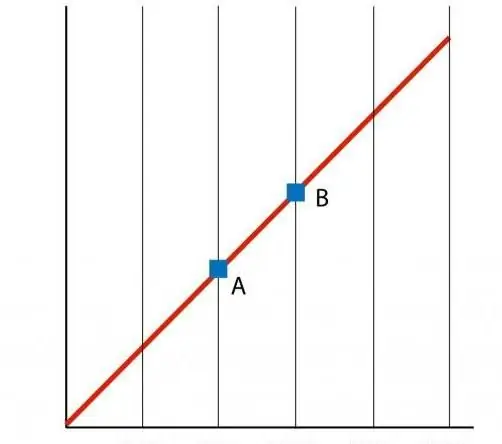
Če zgradimo graf funkcije P(T), dobimo odvisnost ravne črte, ki ji pravimo izohora. Vsaka izohora (za vse vrednosti n in V) je ravna črta.
Energijski opis procesa
Kot že omenjeno, je izohorični proces sprememba stanja sistema, ki poteka v zaprtem, a ne izoliranem sistemu. Govorimo o možnosti izmenjave toplote med plinom in okoljem. Na splošno vsaka dobava toplote Q sistemu vodi do dveh rezultatov:
- spreminja notranjo energijo U;
- plindeluje A, širi se ali krči.
Zadnji sklep je matematično zapisan na naslednji način:
Q=U + A.
Izohorični proces idealnega plina po svoji definiciji ne pomeni dela, ki ga opravi plin, saj njegova prostornina ostane nespremenjena. To pomeni, da vsa toplota, ki se dovaja v sistem, gre za povečanje njegove notranje energije:
Q=U.
Če v ta izraz nadomestimo eksplicitno formulo za notranjo energijo, potem lahko toploto izohoričnega procesa predstavimo kot:
Q=z / 2nRT.
Tukaj je z število svobodnih stopenj, ki je določeno s poliatomsko naravo molekul, ki sestavljajo plin. Za enoatomski plin je z=3, za dvoatomski plin - 5, za triatomski in več - 6. Tu pod svobodnimi stopnjami mislimo translacijske in rotacijske stopnje.
Če primerjamo učinkovitost ogrevanja plinskega sistema v izohoričnih in izobaričnih procesih, potem bomo v prvem primeru dobili največji izkoristek, saj se med izobarično spremembo stanja sistema plin razširi in del vložene toplote se porabi za opravljanje dela.
Izobarični proces
Zgoraj smo podrobno opisali, da je to izohoričen proces. Zdaj pa povejmo nekaj besed o drugih izoprocesih. Začnimo z izobarično. Glede na ime se razume kot prehod sistema med stanji pri konstantnem tlaku. Ta postopek opisuje zakon Gay-Lussac na naslednji način:
V / T=konst.
Tako kot pri izohori, izobar V(T) prav tako predstavlja ravno črto na grafu.
Zakaterega koli izobaričnega procesa je priročno izračunati delo, ki ga opravi plin, saj je enako zmnožku konstantnega tlaka in spremembe prostornine.
Izotermični proces
To je proces, pri katerem temperatura sistema ostane konstantna. Opisuje ga Boyle-Mariotteov zakon za idealni plin. Zanimivo je, da je to prvi eksperimentalno odkrit plinski zakon (druga polovica 17. stoletja). Njegov matematični zapis je videti takole:
PV=konst.
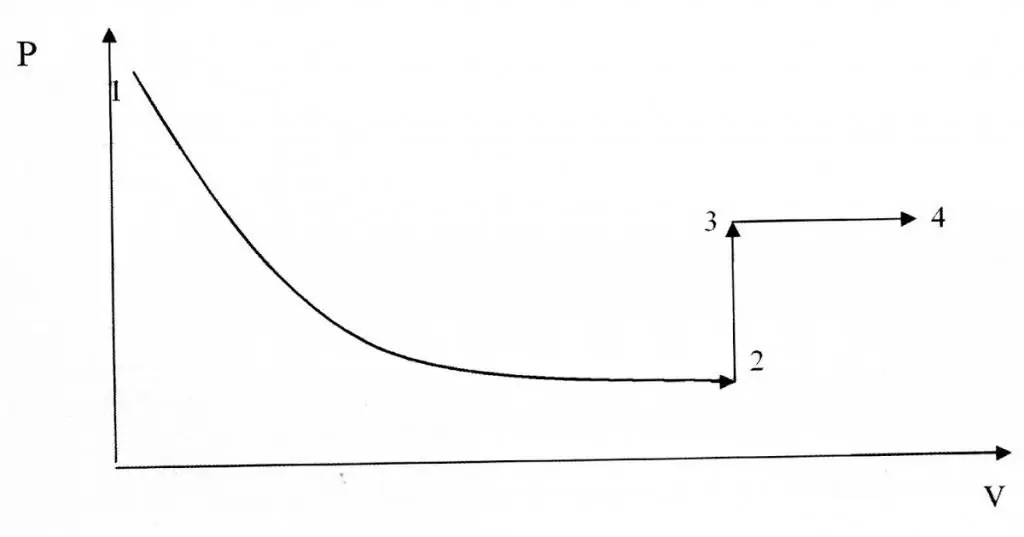
Izohorični in izotermični procesi se razlikujejo glede na grafično predstavitev, saj je funkcija P(V) hiperbolična, ne linearna razmerja.
Primer reševanja problemov
Združimo teoretične informacije v članku z njihovo uporabo za rešitev praktičnega problema. Znano je, da je bil čisti plinasti dušik v jeklenki pri tlaku 1 atmosfere in temperaturi 25 °C. Po segrevanju plinske jeklenke in merjenju tlaka v njej se je izkazalo, da je 1,5 atmosfere. Kakšna je temperatura plina v jeklenki po segrevanju? Za koliko se je spremenila notranja energija plina, če je bilo v balonu 4 mole dušika.
Za odgovor na prvo vprašanje uporabimo naslednji izraz:
P1 / T1=P2 / T 2.
Od kod dobimo:
T2=P2 / P1 T 1.
V tem izrazu lahko tlak nadomestimo v poljubnih enotahmeritve, saj se krčijo, temperatura pa je le v kelvinih. Glede na to dobimo:
T2=1,5 /1298,15=447,224 K.
Izračunana temperatura v stopinjah Celzija je 174 °C.
Ker je molekula dušika dvoatomska, lahko spremembo njene notranje energije med segrevanjem določimo na naslednji način:
ΔU=5 / 2nRΔT.
Če v ta izraz nadomestimo znane vrednosti, bomo dobili odgovor na drugo vprašanje problema: ΔU=+12,4 kJ.






