Vsak človek se v svojem življenju sreča s telesi, ki so v enem od treh agregatnih stanj snovi. Najpreprostejše agregacijsko stanje za preučevanje je plin. V članku bomo obravnavali koncept idealnega plina, dali enačbo stanja sistema in posvetili nekaj pozornosti opisu absolutne temperature.
Plinsko stanje
Vsak študent ima dobro predstavo o tem, o kakšnem agregatnem stanju govori, ko sliši besedo "plin". To besedo razumemo kot telo, ki je sposobno zasesti kateri koli obseg, ki mu je dodeljen. Ne more obdržati svoje oblike, saj se ne more upreti niti najmanjšemu zunanjemu vplivu. Prav tako plin ne zadržuje prostornine, kar ga razlikuje ne le od trdnih snovi, ampak tudi od tekočin.
Kot tekočina je plin tekoča snov. Pri gibanju trdnih teles v plinih slednji to gibanje ovirajo. Nastala sila se imenuje upor. Njegova vrednost je odvisna odhitrost telesa v plinu.
Močni primeri plinov so zrak, zemeljski plin, ki se uporablja za ogrevanje domov in kuhanje, inertni plini (Ne, Ar), ki se uporabljajo za polnjenje reklamnih žarilnih cevi ali se uporabljajo za ustvarjanje inertnega (neagresivnega, zaščitnega) okolja pri varjenju.
Idealni plin
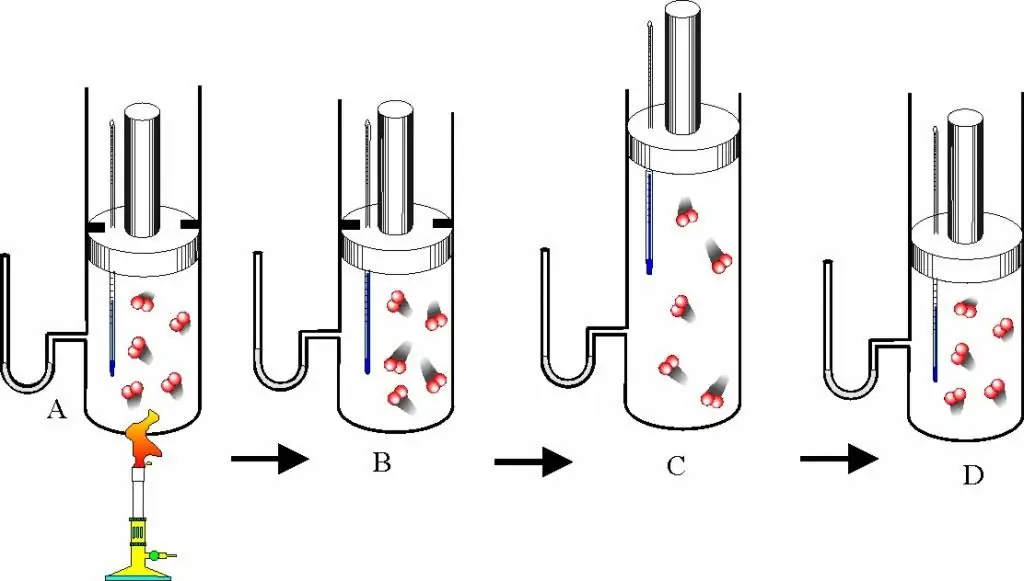
Preden nadaljujete z opisom plinskih zakonov in enačbe stanja, morate dobro razumeti vprašanje, kaj je idealen plin. Ta koncept je uveden v molekularno kinetični teoriji (MKT). Idealen plin je vsak plin, ki izpolnjuje naslednje značilnosti:
- Delci, ki ga tvorijo, ne delujejo drug z drugim, razen pri neposrednih mehanskih trkih.
- Zaradi trka delcev s stenami posode ali med seboj se njihova kinetična energija in zagon ohranita, kar pomeni, da se trk šteje za popolnoma elastičen.
- Delci nimajo dimenzij, imajo pa končno maso, torej so podobni materialnim točkam.
Naravno je, da vsak plin ni idealen, ampak resničen. Kljub temu so ti približki za reševanje številnih praktičnih problemov precej veljavni in jih je mogoče uporabiti. Obstaja splošno empirično pravilo, ki pravi: ne glede na kemično naravo, če ima plin temperaturo nad sobno temperaturo in tlak reda atmosferskega ali nižjega, se lahko šteje za idealnega z visoko natančnostjo in se lahko uporablja za opis to.formula za enačbo stanja idealnega plina.
Clapeyron-Mendeleev zakon
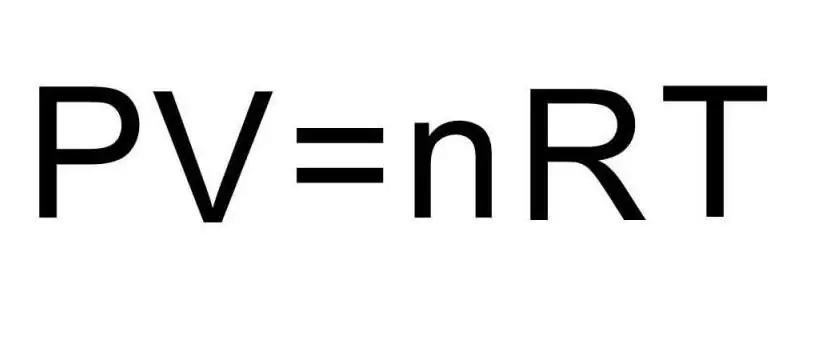
Prehode med različnimi agregatnimi stanji snovi in procesi znotraj enega samega agregatnega stanja obravnava termodinamika. Tlak, temperatura in prostornina so tri količine, ki enolično definirajo katero koli stanje termodinamičnega sistema. Formula za enačbo stanja idealnega plina združuje vse tri te količine v eno samo enačbo. Napišimo to formulo:
PV=nRT
Tukaj P, V, T - tlak, prostornina, temperatura. Vrednost n je količina snovi v molih, simbol R pa označuje univerzalno konstanto plinov. Ta enakost kaže, da večji kot je produkt tlaka in prostornine, večji mora biti produkt količine snovi in temperature.

Formula za enačbo stanja plina se imenuje Clapeyron-Mendeleev zakon. Leta 1834 je francoski znanstvenik Emile Clapeyron, ki je povzemal eksperimentalne rezultate svojih predhodnikov, prišel do te enačbe. Vendar je Clapeyron uporabil številne konstante, ki jih je Mendelejev kasneje zamenjal z eno - univerzalno plinsko konstanto R (8, 314 J / (molK)). Zato je v sodobni fiziki ta enačba poimenovana po imenih francoskih in ruskih znanstvenikov.

Druge oblike enačb
Zgoraj smo napisali Mendeleev-Clapeyronovo enačbo stanja za idealni plin v splošno sprejetih inpriročna oblika. Vendar pa je pri problemih v termodinamiki pogosto potrebna nekoliko drugačna oblika. Spodaj so zapisane še tri formule, ki neposredno izhajajo iz zapisane enačbe:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Te tri enačbe so tudi univerzalne za idealni plin, le da se v njih pojavljajo količine, kot so masa m, molska masa M, gostota ρ in število delcev N, ki sestavljajo sistem. Simbol kB tukaj označuje Boltzmannovo konstanto (1, 3810-23J/K).
Boyle-Mariotte Law
Ko je Clapeyron sestavil svojo enačbo, je temeljil na plinskih zakonih, ki so bili eksperimentalno odkriti pred nekaj desetletji. Eden od njih je Boyle-Mariotteov zakon. Odraža izotermični proces v zaprtem sistemu, zaradi katerega se spreminjajo makroskopski parametri, kot sta tlak in prostornina. Če damo konstanto T in n v enačbo stanja za idealni plin, bo zakon o plinu imel obliko:
P1V1=P2V 2
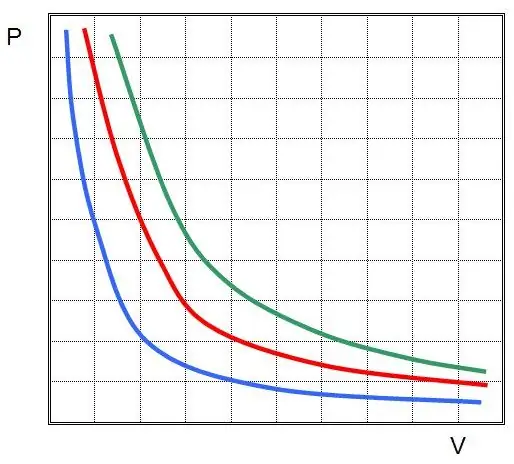
To je Boyle-Mariotteov zakon, ki pravi, da se produkt tlaka in prostornine ohrani med poljubnim izotermnim procesom. V tem primeru se vrednosti P in V sami spremenita.
Če narišete P(V) ali V(P), bodo izoterme hiperbole.
Zakoni Charlesa in Gay-Lussaca
Ti zakoni matematično opisujejo izobarično in izohoričnoprocesi, torej takšni prehodi med stanji plinskega sistema, v katerih se ohranjata tlak in prostornina. Charlesov zakon je mogoče matematično zapisati na naslednji način:
V/T=konst, ko je n, P=konst.
Gay-Lussacov zakon je zapisan takole:
P/T=konst, ko je n, V=konst.
Če sta obe enakosti predstavljeni v obliki grafa, bomo dobili ravne črte, ki so nagnjene pod nekim kotom na os x. Ta vrsta grafa kaže neposredno sorazmernost med prostornino in temperaturo pri konstantnem tlaku ter med tlakom in temperaturo pri konstantni prostornini.
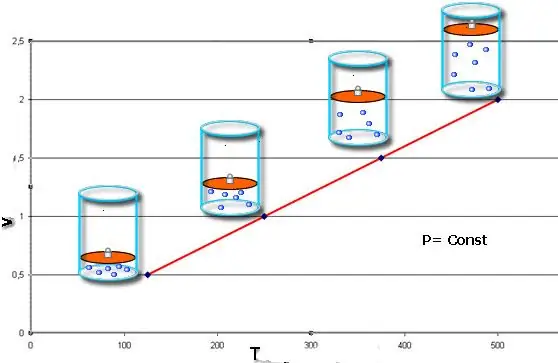
Upoštevajte, da vsi trije obravnavani plinski zakoni ne upoštevajo kemične sestave plina, pa tudi spremembe njegove količine snovi.
Absolutna temperatura
V vsakdanjem življenju smo navajeni uporabljati temperaturno lestvico Celzija, saj je priročna za opis procesov okoli nas. Torej voda zavre pri 100 oC in zamrzne pri 0 oC. V fiziki se ta lestvica izkaže za neprijetno, zato se uporablja tako imenovana absolutna temperaturna lestvica, ki jo je sredi 19. stoletja uvedel Lord Kelvin. V skladu s to lestvico se temperatura meri v Kelvinih (K).
Meni je, da pri temperaturi -273, 15 oC ni toplotnih vibracij atomov in molekul, njihovo gibanje naprej se popolnoma ustavi. Ta temperatura v stopinjah Celzija ustreza absolutni ničli v Kelvinih (0 K). Iz te definicijesledi fizični pomen absolutne temperature: je merilo kinetične energije delcev, ki sestavljajo snov, na primer atomov ali molekul.
Poleg zgornjega fizičnega pomena absolutne temperature obstajajo tudi drugi pristopi k razumevanju te količine. Eden izmed njih je omenjeni Charlesov zakon o plinu. Zapišimo ga v naslednji obliki:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Zadnja enakost pravi, da pri določeni količini snovi v sistemu (na primer 1 mol) in določenem tlaku (na primer 1 Pa) prostornina plina enolično določa absolutno temperaturo. Z drugimi besedami, povečanje prostornine plina v teh pogojih je možno le zaradi zvišanja temperature, zmanjšanje prostornine pa pomeni zmanjšanje vrednosti T.
Ne pozabite, da za razliko od temperature Celzija absolutna temperatura ne more biti negativna.
Avogadro princip in mešanice plinov
Poleg zgornjih plinskih zakonov enačba stanja za idealni plin vodi tudi do načela, ki ga je na začetku 19. stoletja odkril Amedeo Avogadro, ki nosi njegov priimek. To načelo določa, da je prostornina katerega koli plina pri konstantnem tlaku in temperaturi določena s količino snovi v sistemu. Ustrezna formula izgleda takole:
n/V=konst, ko je P, T=konst.
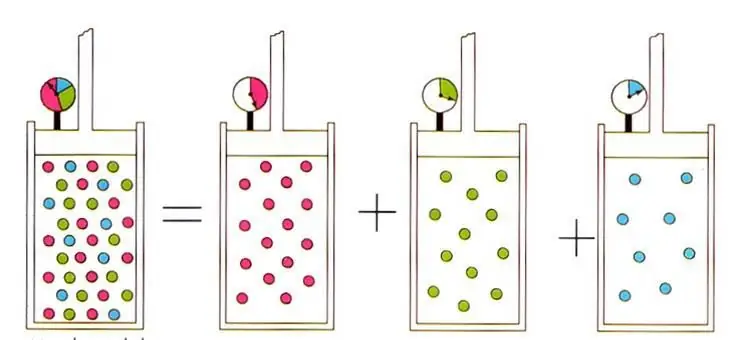
Pisani izraz vodi do dobro znanega v fiziki idealnih plinov D altonovega zakona za plinske zmesi. tolezakon pravi, da je parcialni tlak plina v zmesi enolično določen z njegovim atomskim deležem.
Primer reševanja problemov
V zaprti posodi s trdimi stenami, ki vsebuje idealen plin, se je tlak zaradi segrevanja povečal za 3-krat. Končno temperaturo sistema je treba določiti, če je bila njegova začetna vrednost 25 oC.
Najprej pretvorimo temperaturo iz stopinj Celzija v Kelvin, imamo:
T=25 + 273, 15=298, 15 K.
Ker so stene posode toge, lahko postopek segrevanja štejemo za izohoričen. Za ta primer uporabljamo zakon Gay-Lussaca, imamo:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Tako se končna temperatura določi iz zmnožka razmerja tlaka in začetne temperature. Če zamenjamo podatke z enakostjo, dobimo odgovor: T2=894,45 K. Ta temperatura ustreza 621,3 oC.






