Kot veste, katera koli fizična količina spada v eno od dveh vrst, je bodisi skalarna ali vektorska. V tem članku bomo obravnavali takšne kinematične značilnosti, kot sta hitrost in pospešek, ter pokazali, kam so usmerjeni vektorji pospeška in hitrosti.
Kaj sta hitrost in pospešek?
Obe količini, omenjeni v tem odstavku, sta pomembni značilnosti katere koli vrste gibanja, ne glede na to, ali gre za premikanje telesa v ravni črti ali po ukrivljeni poti.
Hitrost je hitrost, s katero se koordinate spreminjajo skozi čas. Matematično je ta vrednost enaka časovni izpeljanki prevožene razdalje, to je:
v¯=dl¯/dt.
Tukaj je vektor l¯ usmerjen od začetne točke poti do končne točke.
Pospešek pa je hitrost, s katero se sama hitrost spreminja v času. V obliki formule se lahko zapiše takole:
a¯=dv¯/dt.
Očitno jemljemo drugo izpeljanko odvektor premika l¯ v času, dobimo tudi vrednost pospeška.
Ker se hitrost meri v metrih na sekundo, se pospešek po pisnem izrazu meri v metrih na sekundo na kvadrat.

Kje sta vektorja pospeška in hitrosti?
V fiziki je za vsako mehansko gibanje telesa običajno značilna določena pot. Slednje je neka namišljena krivulja, po kateri se telo giblje v prostoru. Na primer, ravna črta ali krog sta najboljša primera običajnih poti gibanja.
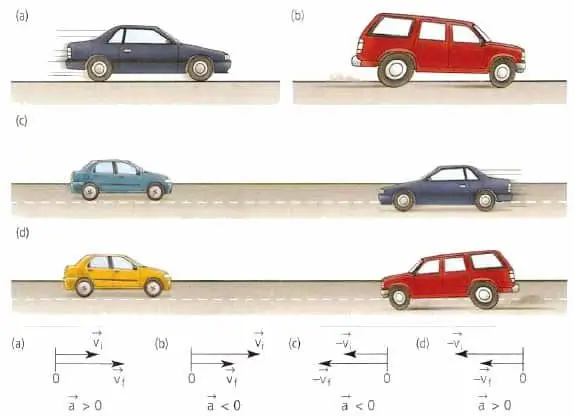
Vektor hitrosti telesa je vedno usmerjen v smeri gibanja, ne glede na to, ali se telo upočasnjuje ali pospešuje, ali se giblje v ravni črti ali po krivulji. Če govorimo geometrijsko, je vektor hitrosti usmerjen tangencialno na točko poti, v kateri se telo trenutno nahaja.
Vektor pospeška materialne ali telesne točke nima nič opraviti s hitrostjo. Ta vektor je usmerjen v smeri spremembe hitrosti. Na primer, pri pravokotnem gibanju lahko vrednost a¯ sovpada v smeri z v¯ ali pa je nasprotna v¯.
Sila, ki deluje na telo in pospešek
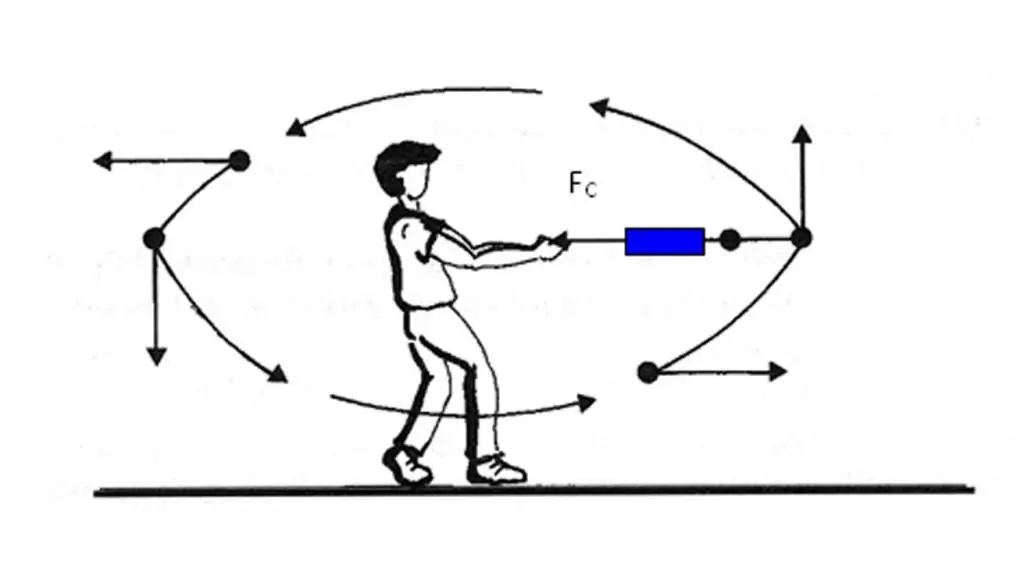
Ugotovili smo, da je vektor pospeška telesa usmerjen proti spremembi vektorja hitrosti. Vendar pa ni vedno lahko določiti, kako se hitrost spreminja na določeni točki poti. Poleg tega je za določitev spremembe hitrosti potrebno izvesti operacijovektorske razlike. Da bi se izognili tem težavam pri določanju smeri vektorja a¯, obstaja še en način, kako hitro ugotoviti.
Spodaj je Newtonov slavni in vsem študentom dobro znan zakon:
F¯=ma¯.
Formula kaže, da je vzrok pospeška v telesih sila, ki nanje deluje. Ker je masa m skalarna, sta vektor sile F¯ in vektor pospeška a¯ v isti smeri. To dejstvo si je treba zapomniti in uporabiti v praksi, kadar koli je treba določiti smer količine a¯.
Če na telo deluje več različnih sil, bo smer vektorja pospeška enaka končnemu vektorju vseh sil.
Krožno gibanje in pospešek
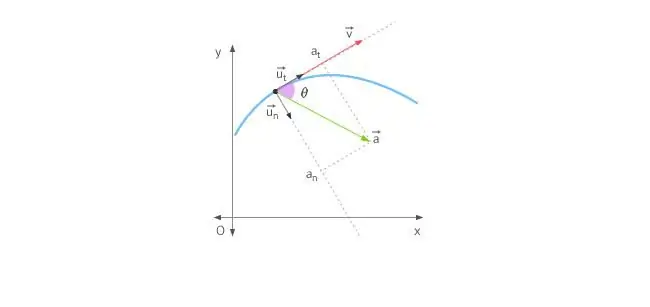
Ko se telo giblje v ravni črti, je pospešek usmerjen naprej ali nazaj. V primeru gibanja v krogu je situacija zapletena zaradi dejstva, da vektor hitrosti nenehno spreminja svojo smer. Glede na zgoraj navedeno je skupni pospešek določen z dvema komponentama: tangencialnim in normalnim pospeškom.
Tangencialni pospešek je usmerjen popolnoma enako kot vektor hitrosti ali proti njemu. Z drugimi besedami, ta komponenta pospeška je usmerjena vzdolž tangente na trajektorijo. Tangencialni pospešek opisuje spremembo modula same hitrosti.
Normalni pospešek je usmerjen vzdolž normale na dano točko poti, ob upoštevanju njene ukrivljenosti. V primeru krožnega gibanja vektor te komponente označujedo središča, to pomeni, da je normalni pospešek usmerjen vzdolž polmera vrtenja. Ta komponenta se pogosto imenuje centripetalna.
Polni pospešek je vsota teh komponent, zato je njegov vektor lahko poljubno usmerjen glede na krožno črto.
Če se telo vrti brez spreminjanja linearne hitrosti, potem obstaja samo normalna komponenta, ki ni nič, zato je vektor celotnega pospeška usmerjen proti središču kroga. Upoštevajte, da na to središče vpliva tudi sila, ki drži telo na poti. Na primer, gravitacijska sila Sonca ohranja našo Zemljo in druge planete v njihovih orbitah.






